Activité théâtrale
DURÉE MOYENNE : 1h30 - 2h
LIEU : théâtre, gymnase ou cour
MATÉRIEL : cerceaux de gymnastique ou hula hoop, cordes, masques de chevaliers et fripons pour chaque élève (téléchargeables dans la section PIÈCES-JOINTES), symboles à coller sur le t-shirt des enfants (téléchargeables dans la section PIÈCES-JOINTES).
La première activité que nous suggérons de proposer est une activité théâtrale propédeutique au parcours BUL.
L’objet principal que l’on utilise lors des activités est le masque : le masque de chevalier, un personnage qui dit toujours la vérité, et celui du fripon, qui ne fait que mentir. Les masques sont téléchargeables et prêts à être imprimés dans la section pièces-jointes en bas de page. L’objectif principal de l’activité est de faire explorer à la classe les concepts de vérité et de fausseté, que ce soit dans un contexte mathématique ou extra-mathématique.
LE CHEVALIER
L’enseignant, après avoir disposée la classe en cercle, donne à chaque élève un masque de chevalier en le présentant comme personnage qui "dit toujours la vérité !". Il se met alors le masque de chevalier et la fait mettre à toute la classe : chacun à son tour, en commençant par l’enseignant, dira une phrase vraie : le soleil est jaune, je m’appelle Virginie (si c’est bien le prénom de l’élève en question), j’ai un pantalon bleu (si le pantalon en question est bien bleu), etc. Après avoir fait un premier tour, on les invite à en faire un autre en disant seulement des énoncés mathématiques : deux plus deux égalent quatre, sept fois huit égalent cinquante-six, trois est supérieur à un, etc.
LE FRIPON
Toujours en cercle, l’enseignant distribue les masques de fripon en le présentant comme personnage qui "dit toujours des mensonges !". Ensuite - et pas avant- il se met le masque de fripon et la fait mettre à toute la classe : chacun son tour en commençant par l’enseignant, dira une phrase fausse : le soleil est vert, je m’appelle Virginie (alors que ce n’est PAS le prénom de l’élève en question), j’ai un pantalon bleu (alors que ce n’est PAS la vraie couleur du pantalon), etc. Nous conseillons à l’enseignant d’être le premier à dire les énoncés mathématiques : deux plus deux égalent huit, sept fois huit égalent quatorze, huit est supérieur à dix, etc.
Il est conseillé de faire plusieurs tours afin que chaque élève puisse dire différents énoncés faux.
DEVINER LE PERSONNAGE
L'enseignant se met alors dos à la classe et - après avoir mis un masque - dira une phrase de son choix en accord avec le masque choisi. La classe devra deviner quel personnage est en train de parler. Le même jeu peut être reproduit par un ou plusieurs élèves. C’est là qu’on peut mettre l’accent sur le fait que la phrase "Je suis un chevalier" peut être prononcée soit par un chevalier - parce qu’il dit toujours la vérité et qu’il s’agit effectivement d’un chevalier - soit par un fripon - parce qu’il ment toujours. De la même manière, la phrase "Je suis un fripon" ne peut être prononcée ni par un cavalier - parce qu’il mentirait - ni par un fripon- parce qu’il dirait la vérité.
On pourrait également - idée compliquée mais intéressante - essayer de proposer des devinettes comme celles de SMULLYAN GAME. Les différents personnages de ces devinettes sont les personnes qui se mettent dos tourné. Dans cette dynamique nous conseillons comme première expérience de proposer une variante où il n’y a que deux interprètes et seul l’un deux parle et dit "Nous sommes tous deux des fripons !".
LES CIRCUITS
Le but du jeu sera de toujours partir d’un cercle BLEU en choisissant un masque et d’arriver, en suivant une corde le long de laquelle il sera impossible de changer de masque, à un cercle ROUGE en portant un masque de chevalier. Pendant le trajet, selon le circuit, on pourra tomber sur des imprévus devant nous faire changer de masque ou autre.
Si la classe est nombreuse, il est conseillé de procéder en organisant plusieurs queues d’élèves avec chacune un parcours.
1. CIRCUIT SIMPLE
Le premier circuit que nous vous suggérons de proposer est un circuit simple ne contenant aucun imprévu pendant le parcours. Chaque élève entre tour à tour dans le cercle BLEU, choisit quel masque porter, suit la corde et arrive dans le cercle ROUGE. Si l’élève arrive dans le cercle rouge en portant un masque de chevalier, il gagne. Rappel : le seul endroit où l’élève peut choisir un masque est le cercle BLEU.
Évidemment, la stratégie gagnante dans ce cas est de partir directement avec le masque de chevalier.
2. CIRCUIT AVEC LA NÉGATION
Dans le deuxième circuit on introduira le concept de négation de manière implicite. Un élève colle sur son t-shirt le symbole de la négation - dans les pièces-jointes avec pour titre NOT.pdf – et se place le long du parcours (si possible dans un cerceau ou à côté d’une quille). Son rôle est de faire changer de masque à celui qui passera : si l’un de ses camarades arrive avec un masque de chevalier – pour pouvoir passer – il devra mettre celui de fripon, si son camarade arrive avec un masque de fripon – pour passer – il devra mettre celui de chevalier.
La stratégie gagnante dans ce cas est de partir du cercle bleu avec le masque de fripon.
Au cours de cette première activité, il n’y aura pas besoin d’utiliser le terme "négation". Il suffira d’expliquer que ce drôle de symbole a l’effet de faire changer de masque à celui qui tombera dessus. Mais on pourra appeler l’élève qui porte ce symbole madame ou monsieur non.
3. LA NÉGATION EN SÉRIE
Dans une variante intéressante du deuxième circuit, il y a plusieurs “élèves négation” l’un après l’autre. La stratégie gagnante sera différente selon le nombre de négations : s’il y a un nombre pair de négations (comme dans le circuit 1 où il y en avait 0), la stratégie gagnante est de partir avec un masque de chevalier et si les négations sont en nombre impair (comme dans le circuit 1 où il y en a 1), la stratégie gagnante est de partir avec un masque de fripon. Ce circuit explore le concept de parité : la stratégie gagnante dépend exclusivement du fait qu’il apparaît un nombre de négations pair ou impair.
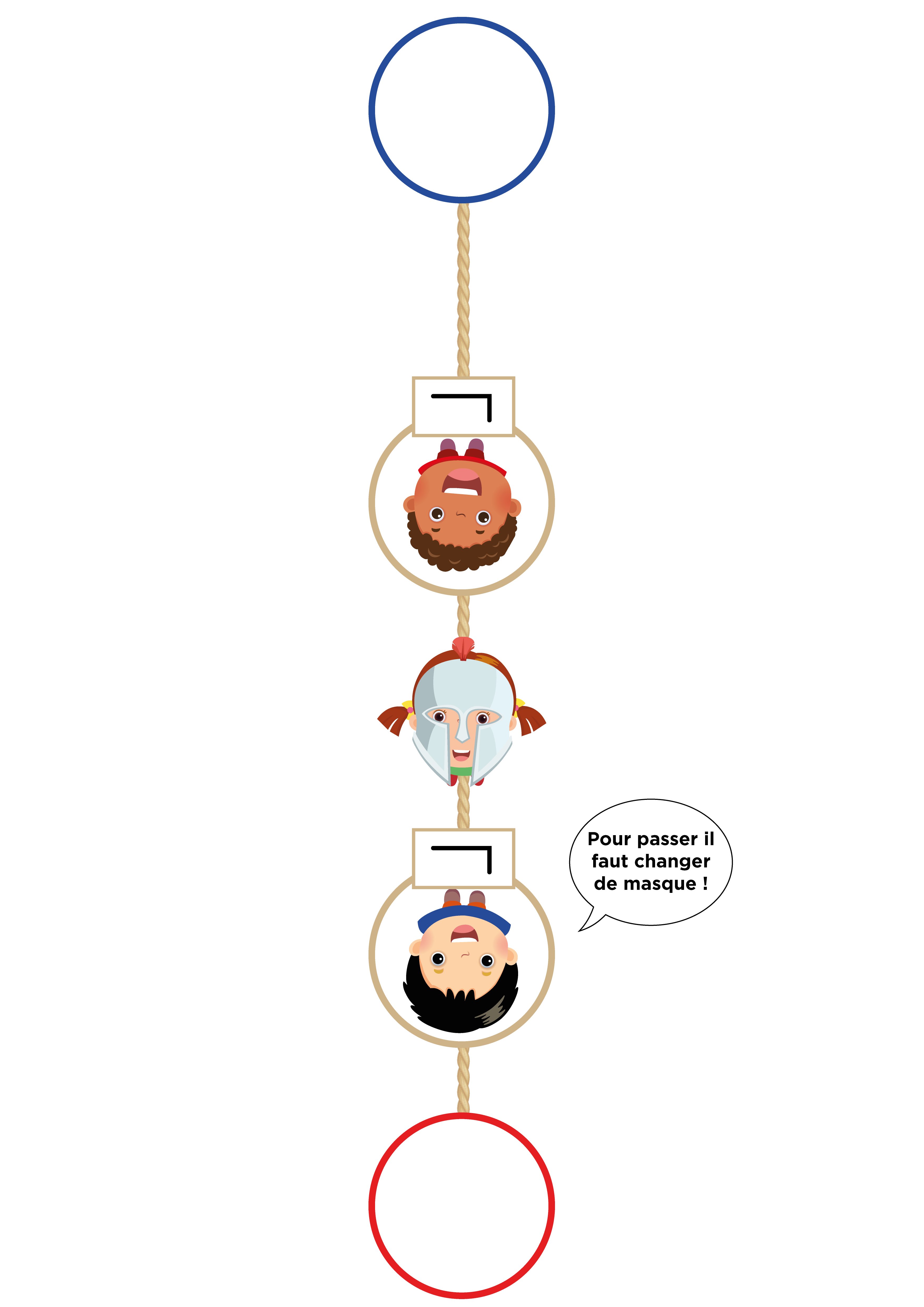
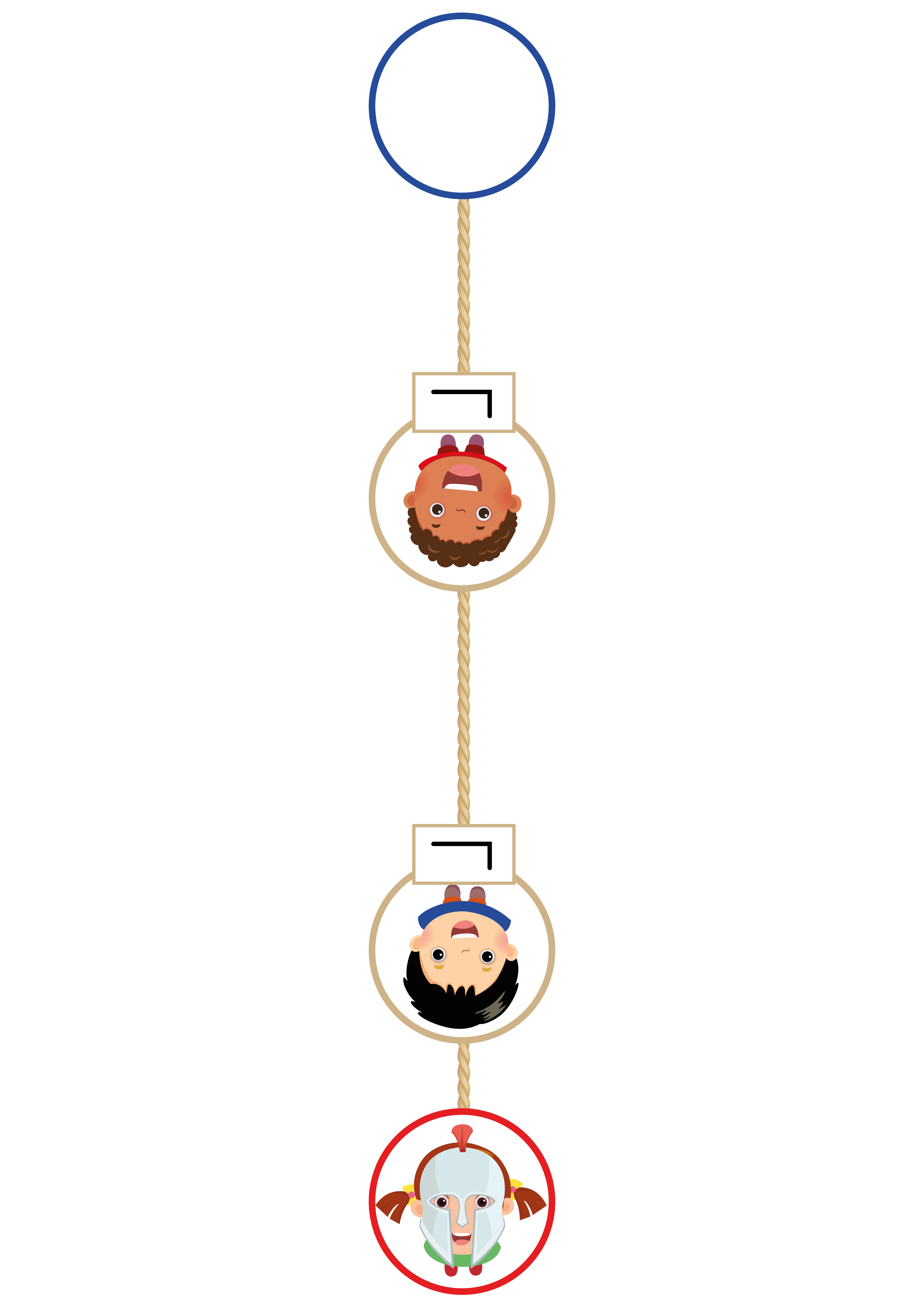
Dans l’exemple représenté sur la figure nous avons deux négations, la stratégie gagnante est donc de partir avec un masque de chevalier.

COLORIER LES PERSONNAGES
Pour terminer l’activité, on peut distribuer à la classe les personnages de chevalier et fripon à colorier, qui se trouvent dans la section pièces-jointes : personnages_a_colorier.pdf.
APPROFONDISSEMENT
Voyons à présent certains circuits plus complexes où l’on rencontre les conjonctions AND et OR. L'enseignant peut choisir de les proposer à la classe ou pas ; s’il décide que oui, il peut le faire même juste avant d’aborder AND et OR avec les activités spécifiques. Il n’est pas opportun, pour le déroulement des circuits, d’expliquer à la classe les significations de AND et de OR : comme pour le NOT, la signification s’apprend ici implicitement.
4. LE CIRCUIT AVEC AND
On augmente désormais pour la première fois le nombre de cercles bleus, et le circuit sera donc parcouru en même temps par plusieurs élèves qui forment une équipe : si dans le cercle rouge (il y en a toujours un seul) c’est le chevalier qui arrive, tous les enfants ayant participé au circuit gagnent. De plus, on y introduit le nouveau symbole AND : l’élève qui portera ce symbole sera à l’intérieur d’un hula hoop avec deux cordes “en entrée” et une “en sortie”. L’“élève AND” préfère les fripons. S’il voit arriver deux fripons il en fera passer un de son choix, s’il voit arriver un fripon et un chevalier il fera passer le fripon et s’il voit arriver deux chevaliers il devra, malgré lui, en faire passer un.
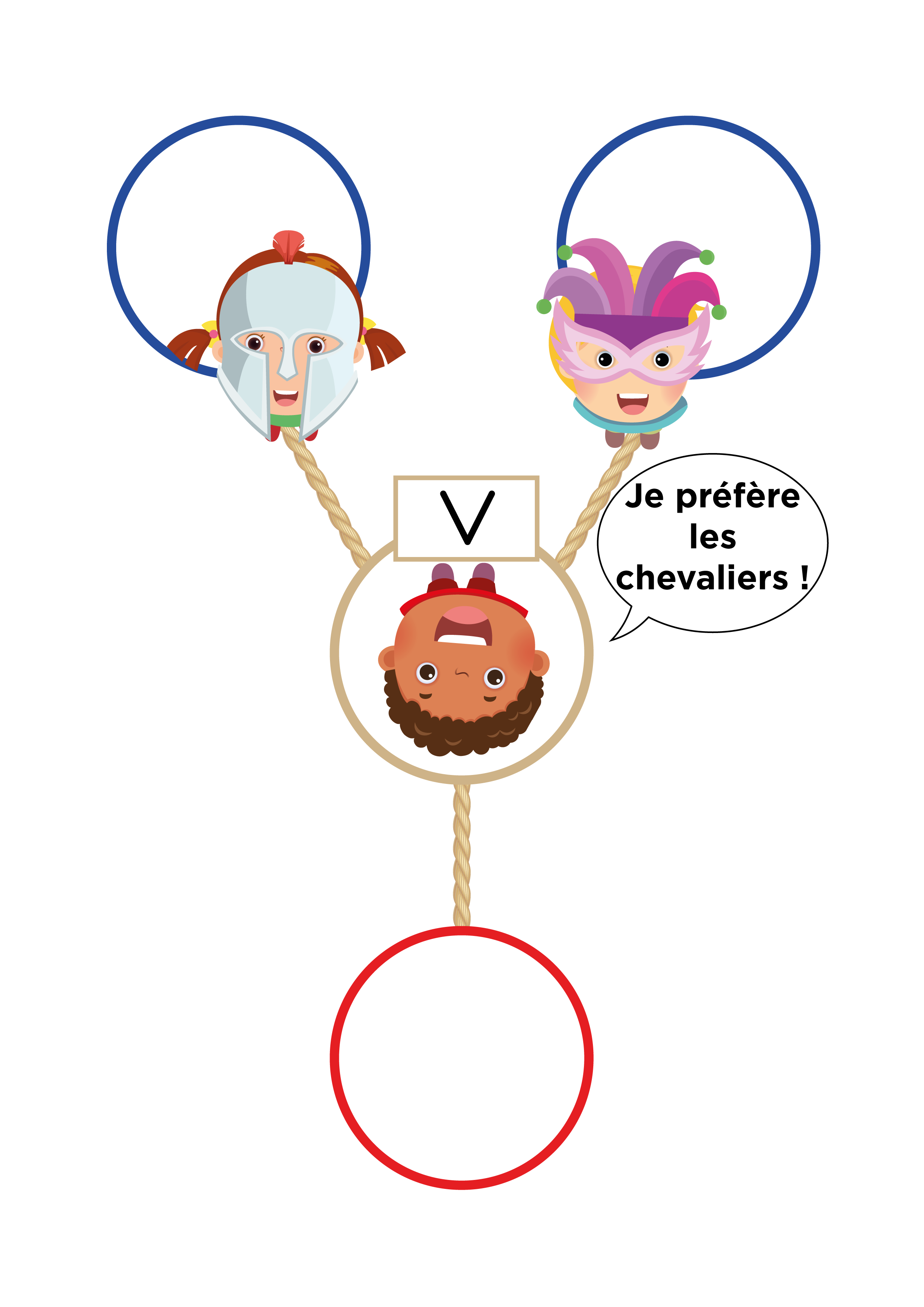
La stratégie gagnante dans ce cas est de partir à deux chevaliers : si même un seul des deux part en tant que fripon, comme l’exemple représenté dans la figure, c’est un fripon qui arrivera dans le cercle rouge.
5. LE CIRCUIT AVEC OR
On introduit le nouveau symbole OR : l’élève qui portera ce symbole sera à l’intérieur d’un hula hoop avec deux cordes “en entrée” et une “en sortie. L’“élève OR” préfère les chevaliers. S’il voit arriver deux chevaliers il en fera passer un de son choix, s’il voit arriver un fripon et un chevalier il fera passer le chevalier et s’il voit arriver deux fripons il devra, malgré lui, en faire passer un.
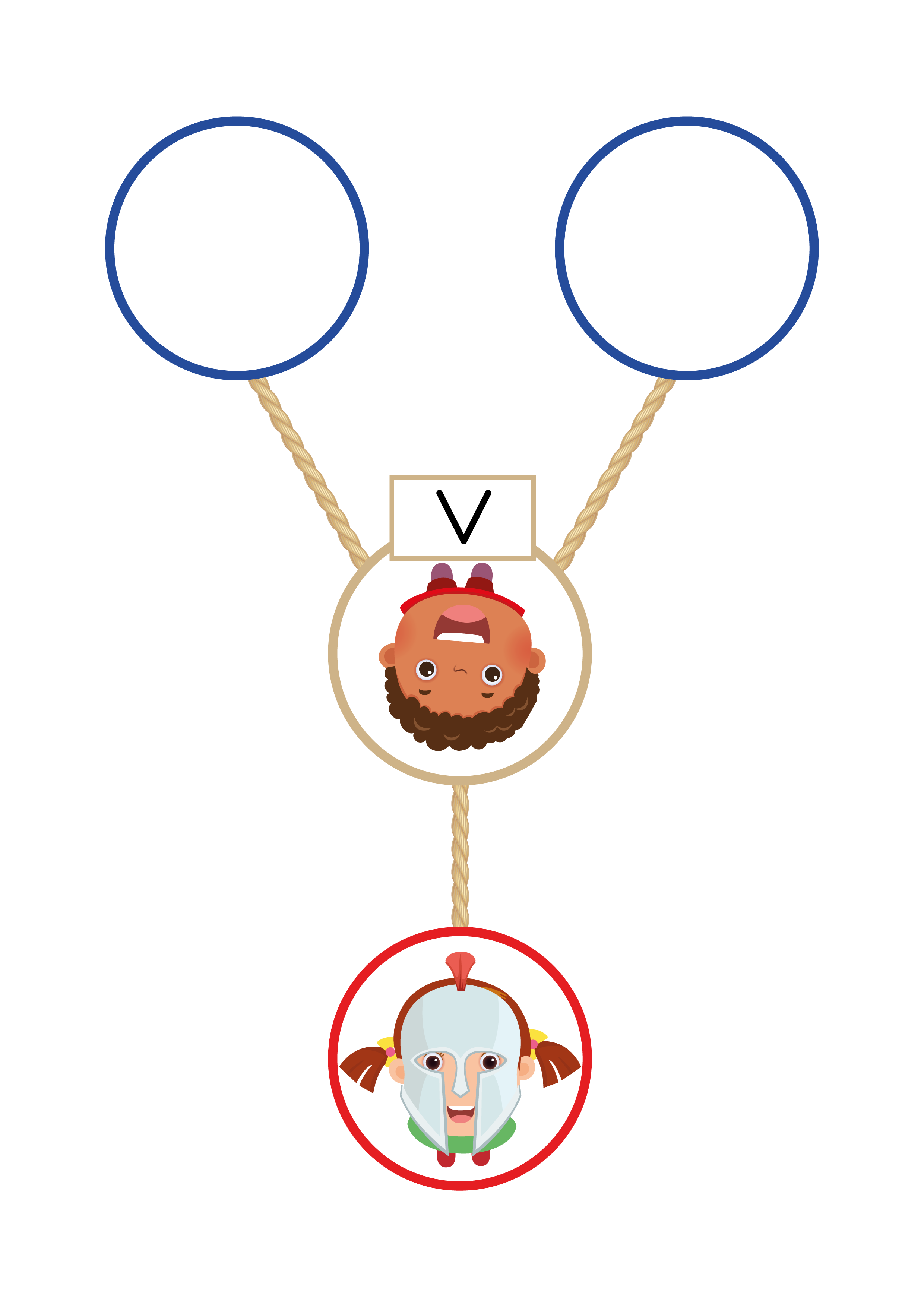
Il y a dans ce cas plusieurs stratégies gagnantes : pour gagner il suffira qu’au moins un des deux élèves soit chevalier et on gagnera alors dans trois cas différents. Le seul cas qui fera perdre l’équipe sera celui où les deux élèves décideront de partir en tant que fripons.
6. CIRCUITS À LOISIR AVEC ENTRÉES À LOISIR
L'enseignant peut à présent décider si proposer à la classe de nouveaux circuits en utilisant simultanément deux symboles ou plus parmi ceux introduits jusqu’alors : soulignons bien que la négation a une corde en entrée et en sortie, tandis que AND et OR ont deux cordes en entrée et une en sortie. De plus, le nombre de cercles rouges sera toujours un et il faudra toujours arriver dans le cercle rouge avec le masque de chevalier. Voir ci-dessous quelques exemples de circuits plus complexes.
Imprimer et découper les masques pour chaque élève requiert un peu de patience. Pour toute suggestion ou demande d’assistance, vous pouvez nous contacter via notre formulaire.
Pièces jointes
Activité théâtrale
DURÉE MOYENNE : 1h30 - 2h
LIEU : théâtre, gymnase ou cour
MATÉRIEL : cerceaux de gymnastique ou hula hoop, cordes, masques de chevaliers et fripons pour chaque élève (téléchargeables dans la section PIÈCES-JOINTES), symboles à coller sur le t-shirt des enfants (téléchargeables dans la section PIÈCES-JOINTES).
La première activité que nous suggérons de proposer est une activité théâtrale propédeutique au parcours BUL.
L’objet principal que l’on utilise lors des activités est le masque : le masque de chevalier, un personnage qui dit toujours la vérité, et celui du fripon, qui ne fait que mentir. Les masques sont téléchargeables et prêts à être imprimés dans la section pièces-jointes en bas de page. L’objectif principal de l’activité est de faire explorer à la classe les concepts de vérité et de fausseté, que ce soit dans un contexte mathématique ou extra-mathématique.
LE CHEVALIER
L’enseignant, après avoir disposée la classe en cercle, donne à chaque élève un masque de chevalier en le présentant comme personnage qui "dit toujours la vérité !". Il se met alors le masque de chevalier et la fait mettre à toute la classe : chacun à son tour, en commençant par l’enseignant, dira une phrase vraie : le soleil est jaune, je m’appelle Virginie (si c’est bien le prénom de l’élève en question), j’ai un pantalon bleu (si le pantalon en question est bien bleu), etc. Après avoir fait un premier tour, on les invite à en faire un autre en disant seulement des énoncés mathématiques : deux plus deux égalent quatre, sept fois huit égalent cinquante-six, trois est supérieur à un, etc.
LE FRIPON
Toujours en cercle, l’enseignant distribue les masques de fripon en le présentant comme personnage qui "dit toujours des mensonges !". Ensuite - et pas avant- il se met le masque de fripon et la fait mettre à toute la classe : chacun son tour en commençant par l’enseignant, dira une phrase fausse : le soleil est vert, je m’appelle Virginie (alors que ce n’est PAS le prénom de l’élève en question), j’ai un pantalon bleu (alors que ce n’est PAS la vraie couleur du pantalon), etc. Nous conseillons à l’enseignant d’être le premier à dire les énoncés mathématiques : deux plus deux égalent huit, sept fois huit égalent quatorze, huit est supérieur à dix, etc.
Il est conseillé de faire plusieurs tours afin que chaque élève puisse dire différents énoncés faux.
DEVINER LE PERSONNAGE
L'enseignant se met alors dos à la classe et - après avoir mis un masque - dira une phrase de son choix en accord avec le masque choisi. La classe devra deviner quel personnage est en train de parler. Le même jeu peut être reproduit par un ou plusieurs élèves. C’est là qu’on peut mettre l’accent sur le fait que la phrase "Je suis un chevalier" peut être prononcée soit par un chevalier - parce qu’il dit toujours la vérité et qu’il s’agit effectivement d’un chevalier - soit par un fripon - parce qu’il ment toujours. De la même manière, la phrase "Je suis un fripon" ne peut être prononcée ni par un cavalier - parce qu’il mentirait - ni par un fripon- parce qu’il dirait la vérité.
On pourrait également - idée compliquée mais intéressante - essayer de proposer des devinettes comme celles de SMULLYAN GAME. Les différents personnages de ces devinettes sont les personnes qui se mettent dos tourné. Dans cette dynamique nous conseillons comme première expérience de proposer une variante où il n’y a que deux interprètes et seul l’un deux parle et dit "Nous sommes tous deux des fripons !".
LES CIRCUITS
Le but du jeu sera de toujours partir d’un cercle BLEU en choisissant un masque et d’arriver, en suivant une corde le long de laquelle il sera impossible de changer de masque, à un cercle ROUGE en portant un masque de chevalier. Pendant le trajet, selon le circuit, on pourra tomber sur des imprévus devant nous faire changer de masque ou autre.
Si la classe est nombreuse, il est conseillé de procéder en organisant plusieurs queues d’élèves avec chacune un parcours.
1. CIRCUIT SIMPLE
Le premier circuit que nous vous suggérons de proposer est un circuit simple ne contenant aucun imprévu pendant le parcours. Chaque élève entre tour à tour dans le cercle BLEU, choisit quel masque porter, suit la corde et arrive dans le cercle ROUGE. Si l’élève arrive dans le cercle rouge en portant un masque de chevalier, il gagne. Rappel : le seul endroit où l’élève peut choisir un masque est le cercle BLEU.
Évidemment, la stratégie gagnante dans ce cas est de partir directement avec le masque de chevalier.
2. CIRCUIT AVEC LA NÉGATION
Dans le deuxième circuit on introduira le concept de négation de manière implicite. Un élève colle sur son t-shirt le symbole de la négation - dans les pièces-jointes avec pour titre NOT.pdf – et se place le long du parcours (si possible dans un cerceau ou à côté d’une quille). Son rôle est de faire changer de masque à celui qui passera : si l’un de ses camarades arrive avec un masque de chevalier – pour pouvoir passer – il devra mettre celui de fripon, si son camarade arrive avec un masque de fripon – pour passer – il devra mettre celui de chevalier.
La stratégie gagnante dans ce cas est de partir du cercle bleu avec le masque de fripon.
Au cours de cette première activité, il n’y aura pas besoin d’utiliser le terme "négation". Il suffira d’expliquer que ce drôle de symbole a l’effet de faire changer de masque à celui qui tombera dessus. Mais on pourra appeler l’élève qui porte ce symbole madame ou monsieur non.
3. LA NÉGATION EN SÉRIE
Dans une variante intéressante du deuxième circuit, il y a plusieurs “élèves négation” l’un après l’autre. La stratégie gagnante sera différente selon le nombre de négations : s’il y a un nombre pair de négations (comme dans le circuit 1 où il y en avait 0), la stratégie gagnante est de partir avec un masque de chevalier et si les négations sont en nombre impair (comme dans le circuit 1 où il y en a 1), la stratégie gagnante est de partir avec un masque de fripon. Ce circuit explore le concept de parité : la stratégie gagnante dépend exclusivement du fait qu’il apparaît un nombre de négations pair ou impair.
Dans l’exemple représenté sur la figure nous avons deux négations, la stratégie gagnante est donc de partir avec un masque de chevalier.



COLORIER LES PERSONNAGES
Pour terminer l’activité, on peut distribuer à la classe les personnages de chevalier et fripon à colorier, qui se trouvent dans la section pièces-jointes : personnages_a_colorier.pdf.
APPROFONDISSEMENT
Voyons à présent certains circuits plus complexes où l’on rencontre les conjonctions AND et OR. L'enseignant peut choisir de les proposer à la classe ou pas ; s’il décide que oui, il peut le faire même juste avant d’aborder AND et OR avec les activités spécifiques. Il n’est pas opportun, pour le déroulement des circuits, d’expliquer à la classe les significations de AND et de OR : comme pour le NOT, la signification s’apprend ici implicitement.
4. LE CIRCUIT AVEC AND
On augmente désormais pour la première fois le nombre de cercles bleus, et le circuit sera donc parcouru en même temps par plusieurs élèves qui forment une équipe : si dans le cercle rouge (il y en a toujours un seul) c’est le chevalier qui arrive, tous les enfants ayant participé au circuit gagnent. De plus, on y introduit le nouveau symbole AND : l’élève qui portera ce symbole sera à l’intérieur d’un hula hoop avec deux cordes “en entrée” et une “en sortie”. L’“élève AND” préfère les fripons. S’il voit arriver deux fripons il en fera passer un de son choix, s’il voit arriver un fripon et un chevalier il fera passer le fripon et s’il voit arriver deux chevaliers il devra, malgré lui, en faire passer un.
La stratégie gagnante dans ce cas est de partir à deux chevaliers : si même un seul des deux part en tant que fripon, comme l’exemple représenté dans la figure, c’est un fripon qui arrivera dans le cercle rouge.
5. LE CIRCUIT AVEC OR
On introduit le nouveau symbole OR : l’élève qui portera ce symbole sera à l’intérieur d’un hula hoop avec deux cordes “en entrée” et une “en sortie. L’“élève OR” préfère les chevaliers. S’il voit arriver deux chevaliers il en fera passer un de son choix, s’il voit arriver un fripon et un chevalier il fera passer le chevalier et s’il voit arriver deux fripons il devra, malgré lui, en faire passer un.
Il y a dans ce cas plusieurs stratégies gagnantes : pour gagner il suffira qu’au moins un des deux élèves soit chevalier et on gagnera alors dans trois cas différents. Le seul cas qui fera perdre l’équipe sera celui où les deux élèves décideront de partir en tant que fripons.


6. CIRCUITS À LOISIR AVEC ENTRÉES À LOISIR
L'enseignant peut à présent décider si proposer à la classe de nouveaux circuits en utilisant simultanément deux symboles ou plus parmi ceux introduits jusqu’alors : soulignons bien que la négation a une corde en entrée et en sortie, tandis que AND et OR ont deux cordes en entrée et une en sortie. De plus, le nombre de cercles rouges sera toujours un et il faudra toujours arriver dans le cercle rouge avec le masque de chevalier. Voir ci-dessous quelques exemples de circuits plus complexes.
Imprimer et découper les masques pour chaque élève requiert un peu de patience. Pour toute suggestion ou demande d’assistance, vous pouvez nous contacter via notre formulaire.
Pièces jointes