Catalogue de tessellations
Une partition - plus exactement un
groupe d'isométrie plate
- est une classification mathématique d'un motif qui se répète sur deux dimensions. Ces motifs
apparaissent fréquemment dans l'architecture et l'art, notamment dans les tissus, les carreaux
et le papier peint.
Vous trouverez ci-dessous toutes les 17 partitions possibles nommées avec la notation
cristallographique, et une méthode (et non la seule) pour les reproduire [1].
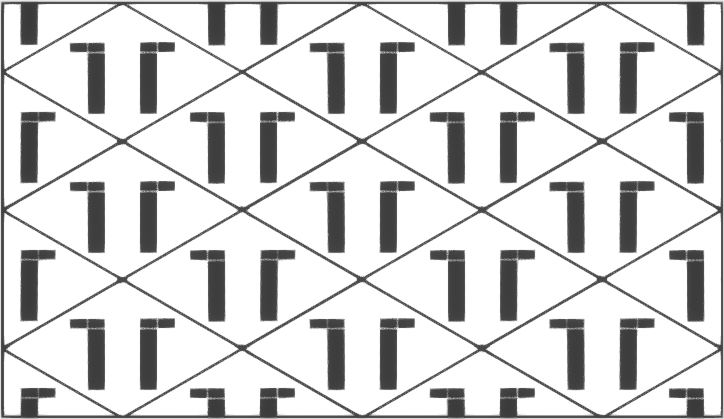
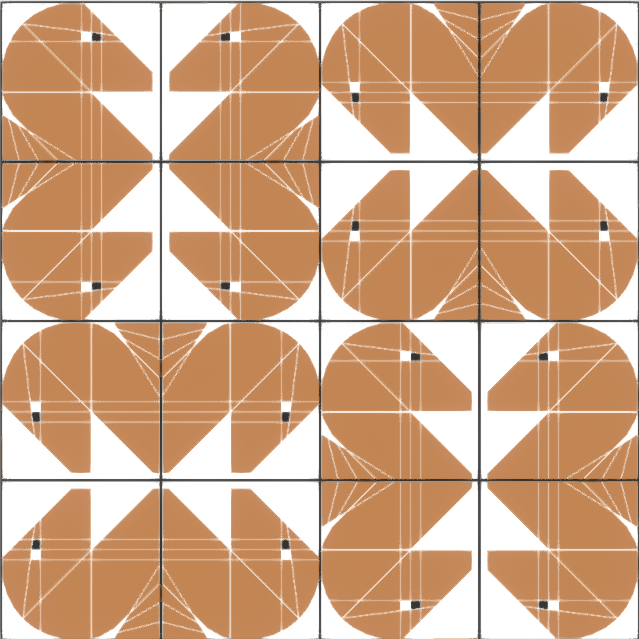
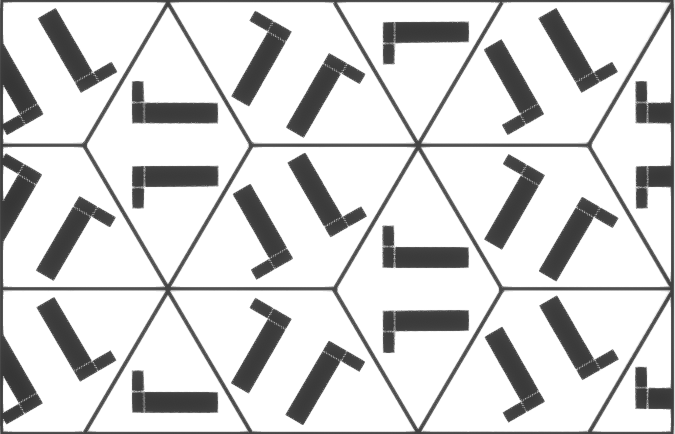
p1

Figure à sélectionner:
carré, rectangle ou losange.
Configuration interne de la pièce:
libre, sans symétries internes.
Tessellation:
la cheville se répète elle-même par translation dans les deux sens.

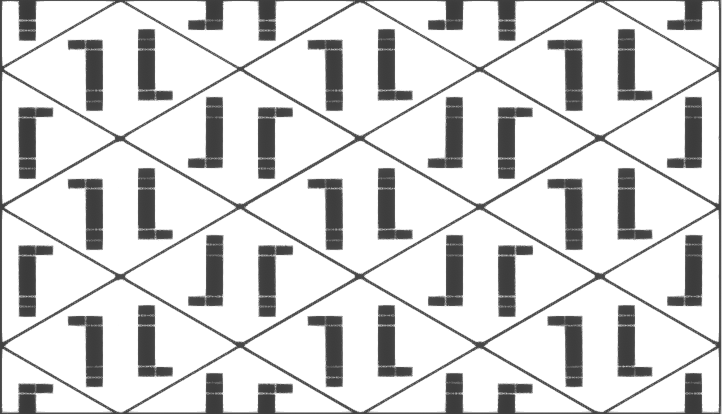
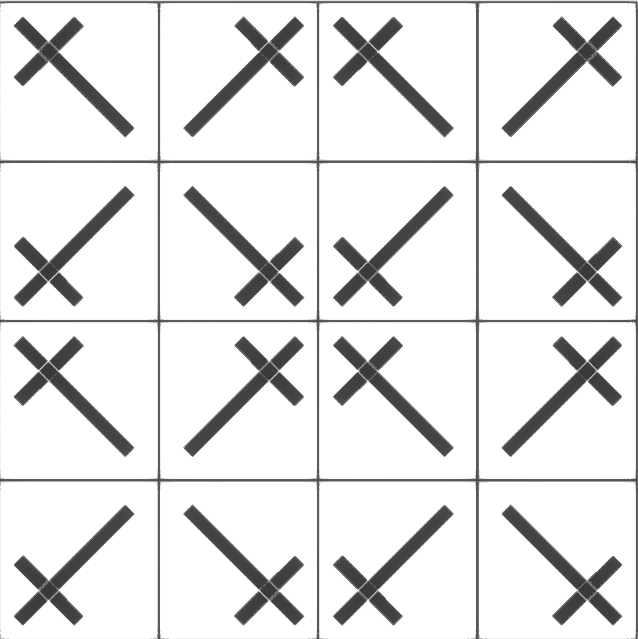
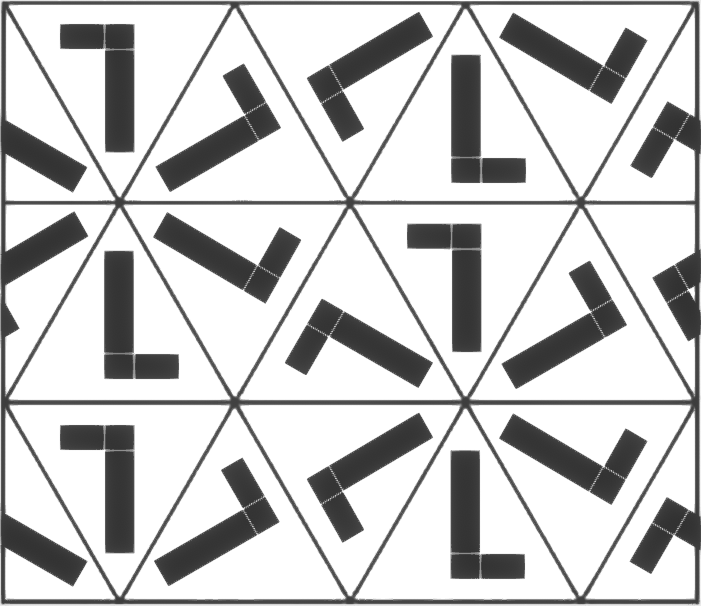
pg

Figure à sélectionner:
carré ou rectangle.
Configuration interne de la pièce:
libre, sans symétries internes.
Tessellation:
la cheville se répète elle-même par translation dans une direction, tandis que sur l'autre elle se réfléchit.

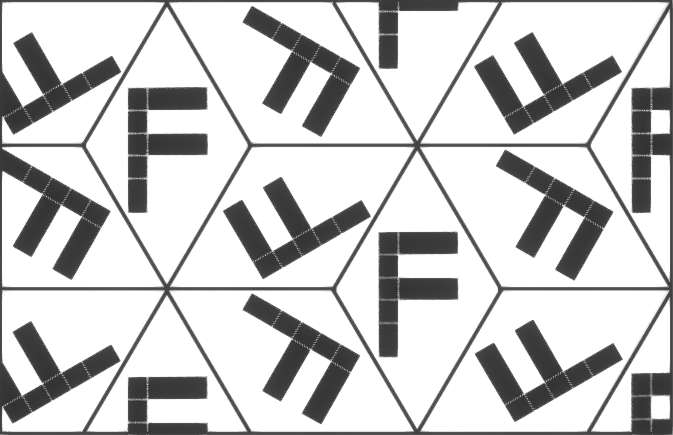
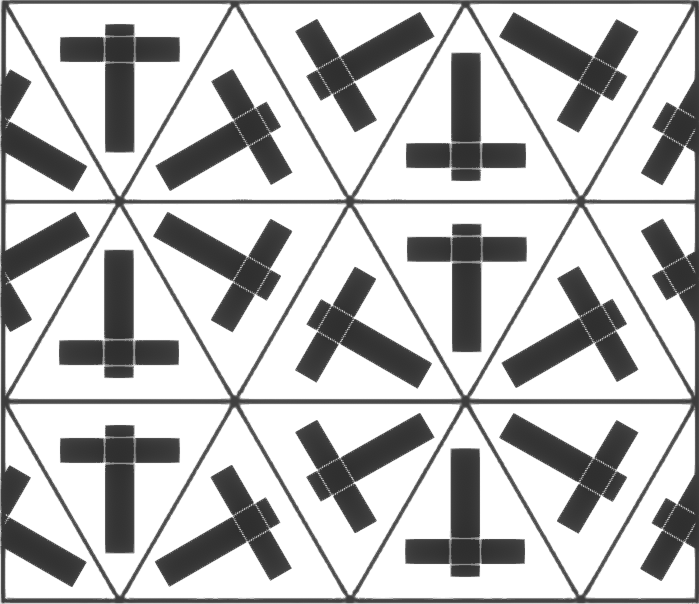
pm

Figure à sélectionner:
carré ou rectangle.
Configuration interne de la pièce:
libre, sans symétries internes.
Tessellation:
la cheville se répète elle-même par translation dans une direction, tandis que sur l'autre elle se réfléchit.

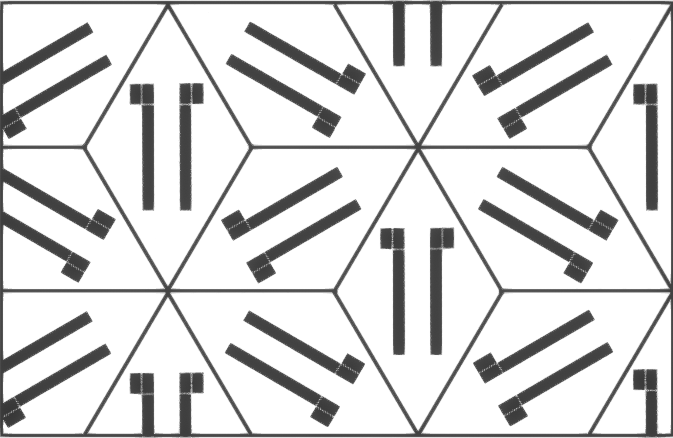
p2

Figure à sélectionner:
carré, rectangle ou losange.
Configuration interne de la pièce:
libre, sans symétries internes.
Tessellation:
la cheville se répète elle-même dans une direction, tandis que dans l'autre elle se modifie selon une symétrie centrale.

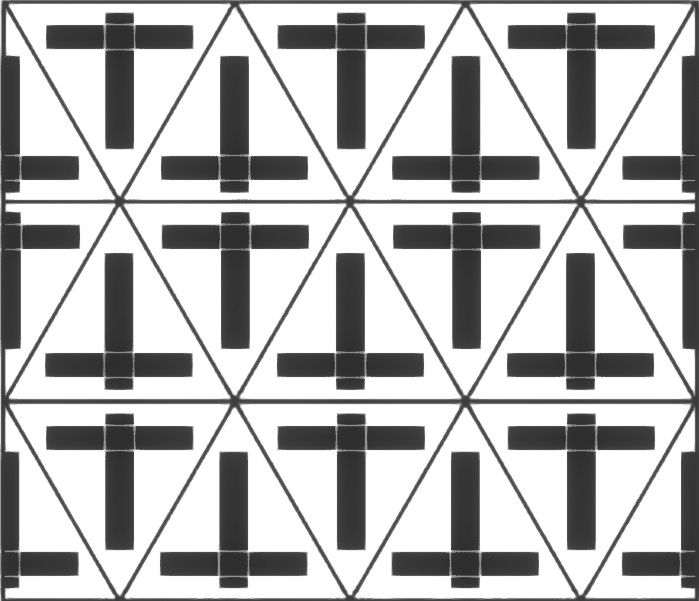
pmm

Figure à sélectionner:
carré ou rectangle.
Configuration interne de la pièce:
libre, sans symétries internes.
Tessellation:
les quatre éléments "regardent" tous vers le sommet commun.

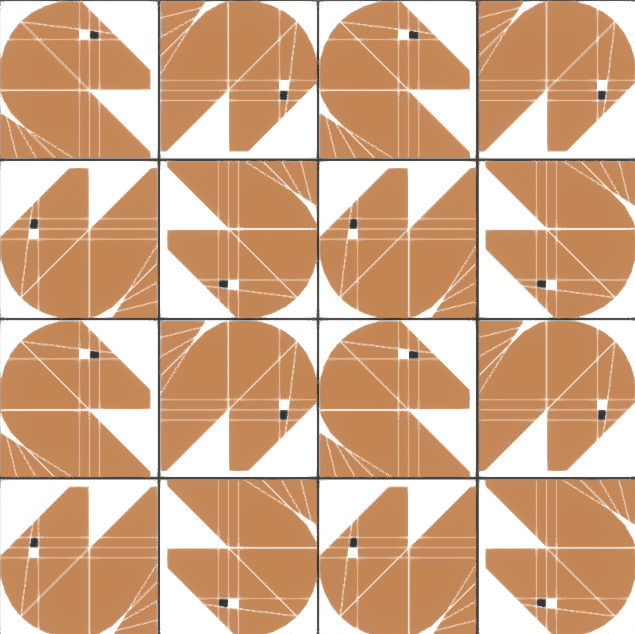
pmg

Figure à sélectionner:
carré ou rectangle.
Configuration interne de la pièce:
symétrie par rapport à une conjonction des points moyens.
Tessellation:
la cheville se répète elle-même par translation dans une direction, tandis que sur l'autre elle se réfléchit.